はじめに
3×3行列以上の逆行列を求めるには「掃き出し法」と「余因子を用いた方法」で逆行列を求めることができます。
この記事では掃き出し法を用いて3×3行列の逆行列の求め方について説明します。
掃き出し法とは
掃き出し法
ある正方行列Aの右側に単位行列Iを加え[A I]とする。[A I]を行基本変形し[I B]の形に変形する。
この行列BがAの逆行列![]() である。
である。
例題
それでは掃き出し法を使って実際に問題を解いてみましょう。
例題
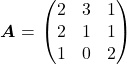 の逆行列
の逆行列![]() を求めよ。
を求めよ。
例題の解説
行列![]() の右側に単位行列を加えます。
の右側に単位行列を加えます。
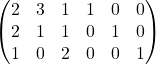
この行列に対し行基本変形します。
1行目と3行目を入れ替えます。
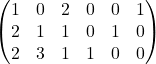
2行目に(-2)倍した1行目を加えます。
3行目に(-3)倍した1行目を加えます。
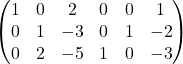
3行目に(-2)倍した2行目を加えます。
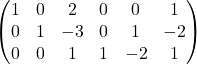
1行目に(-2)倍した3行目を加えます。
2行目に(3)倍した3行目を加えます。
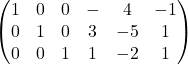
これで[I B]の形に変形することができました。
よって行列![]() の逆行列
の逆行列![]() は、
は、
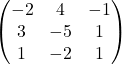 となる。
となる。
追記
今回は、掃き出し法を用いて3×3行列の逆行列の求め方について解説しました。
計算量は多くなりますが、4×4以上の行列の場合も同様の求め方でできます。

