2×2行列の逆行列の求め方と例題

求め方
例題
例題の解説
追記

求め方

2×2行列の逆行列を求める場合は以下の公式を用いることで簡単に求めることが可能です。

2×2行列の逆行列の公式

${\boldsymbol A} = \begin{pmatrix}a&b\\c&d\end{pmatrix}$ の逆行列( ${\boldsymbol A}^{-1}$ )は， ${\boldsymbol A}^{-1} = \dfrac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$
で求めることが可能です。

例題

それでは上記の公式を使用して実際に問題を解いてみましょう。

例題

${\boldsymbol A} = \begin{pmatrix}1&2\\3&4\end{pmatrix}$ の逆行列を求めよ。

例題の解説

公式に当てはめて求めます。

$\dfrac{1}{ad-bc}$ に実際に数値を入れると、 $\dfrac{1}{1\cdot4-2\cdot3} = -\dfrac{1}{2}$ となります。

$\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$ に実際に数値を入れると、 $\begin{pmatrix}4&-2\\-3&1\end{pmatrix}$ となります。

よって答えは、

${\boldsymbol A}^{-1} = -\dfrac{1}{2}\begin{pmatrix}4&-2\\-3&1\end{pmatrix}$ となります。

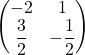$-\dfrac{1}{2}$ を中に入れて、 $\begin{pmatrix}-2&1\\ \dfrac{3}{2}&-\dfrac{1}{2}\end{pmatrix}$ とするのもよいです。

追記

今回は、2×2行列の逆行列の求め方について解説しましたが、3×3以上の行列の場合は、
掃き出し法と余因子を用いた方法で逆行列を求めます。